PythonとFletで相関を持つアセットの資産推移のモンテカルロシミュレーションを行うGUIツールを開発して資産運用シミュレーションを行ってみた
新NISAで盛り上がる資産運用について気になったので、金融に関しては素人ですがプログラムをかいてランダムシミュレーションを行って見ることにしました。 このためにPythonのGUIフレームワークであるFletと、数値計算ライブラリであるnumpyを用いて、相関を持つアセットの資産推移モンテカルロシミュレーションを行うGUIツールを開発してみました。 このツールを用いて、資産運用シミュレーションを行った場合に確率的にはどの程度の振れ幅が出るのかということを見てみました。
スポンサーリンク
開発の経緯
新NISAで盛り上がる資産運用について軽く調べてみると、資産ごとにリスクとリターンが存在していて正規分布の標準偏差と平均にあてはめて色々と計算がされているようでした。ただし、実態は厳密に正規分布ではなくて、ベルカーブの裾野が正規分布より広いテールファットな分布らしいですが、計算を簡略化する場合には正規分布と仮定している場合も多いです。その分現実からはずれるわけですが。
資産運用シミュレーションみたいなWebツールを色々見てみると、資産は1種類としてリターンのみを入力、あるいはリターンとリスクを入力して将来の資産をシミュレーションするというものが多くあります。ただ、資産は種類によってリスクもリターンも異なるものですし、さらに資産は独立しておらず相互に相関を持つものと考えられるのでシミュレーションとしては不十分です。
そのため、実際に自分でプログラムを書いて相関を持つアセットを対象に資産推移シミュレーションが行えるツールを作成することにしました。
注意事項
あらかじめ注意事項として記載しておきますが、本記事・プログラムは資産運用を推奨するものではありません。
筆者は金融には素人ですし、正規分布の仮定とランダムシミュレーションを行っている程度の簡単なプログラムなため、実装方法と結果に理論的な裏付けもありません。
あくまで興味本位でプログラムを作成したに過ぎないので、このツールの結果を用いて資産運用を行ったことで損をしても何の保証もできません。
これらの注意事項をご理解いただいたうえでお読みください。
プログラムの概要
numpyにおけるmultivariate_normal()↗関数を用いることで、相関を持つ正規分布のランダムシミュレーションが行えます。ただし、対称行列かつ半正定値行列であることが前提であることに注意で、これを満たさない場合は結果が保証されないようです。
本GUIツールではこの関数を用いて、ランダムシミュレーションを何度も行うことで資産推移のシミュレーションを行っています。
設定項目としては資産種別ごとのリスク・リターンとその相関、それらの構成比率、運用年数、積立金額と運用年数などが入力でき、運用年数が経過した際の利益率が確認できるものとなっています。
シミュレーションの実行
利用したデータ
年金の運用を行っているGPIFが公開した資料では、2020年4月1日に適用した基本ポートフォリオでは相関係数行列とリスク・リターンを以下のように設定されているとのことでした。(リンク↗)
| 相関係数 | 国内債券 | 外国債券 | 国内株式 | 外国株式 |
|---|---|---|---|---|
| 国内債券 | 1.00 | |||
| 外国債券 | 0.290 | 1.00 | ||
| 国内株式 | -0.158 | 0.060 | 1.00 | |
| 外国株式 | 0.105 | 0.585 | 0.643 | 1.00 |
また、標準偏差と期待リターンは、以下のように設定されている。(名目賃金上昇率2.3%を減算した値)
| 国内債券 | 外国債券 | 国内株式 | 外国株式 | |
|---|---|---|---|---|
| 標準偏差[%] | 2.56 | 11.87 | 23.14 | 24.85 |
| 期待リターン(名目)[%] | 0.7 | 2.6 | 5.6 | 7.2 |
| 期待リターン(実質)[%] | -1.6 | 0.3 | 3.3 | 4.9 |
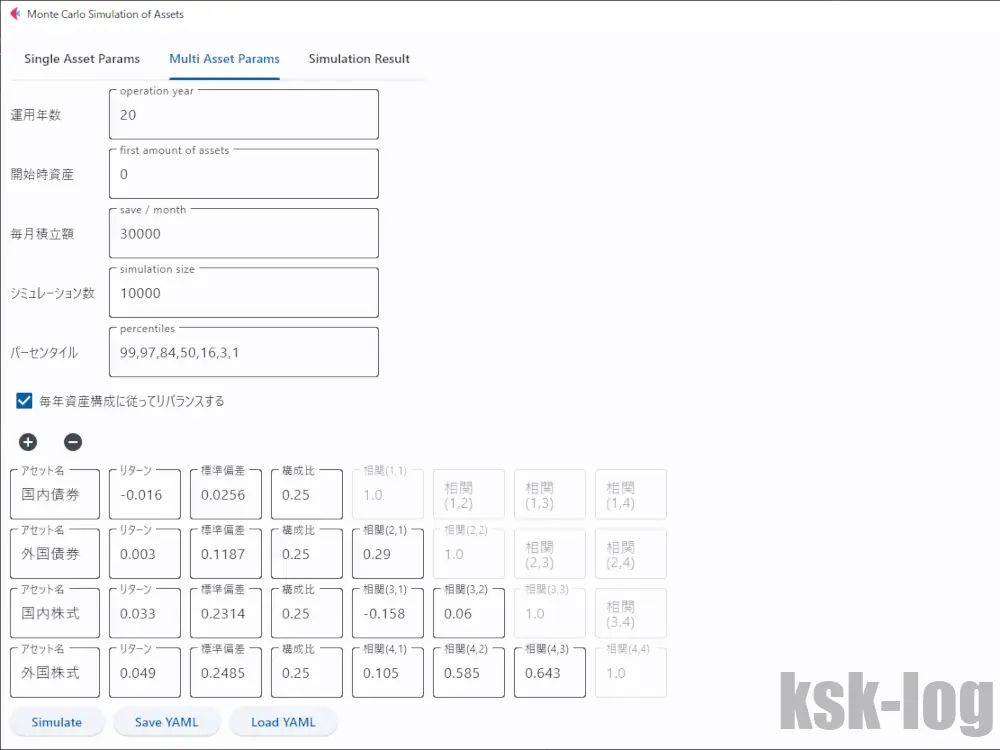
上記のうち、実質リターンを使ってツールに入力してみます。設定条件としては以下の通りです。
- 相関係数行列、リスク、リターンはGPIFのデータを利用する
- 国内債券、外国債券、国内株式、外国株式の比率はすべて25%ずつとする
- 年1回上記の比率となるように資産をリバランスする(税金未考慮)
- 毎月の積立額は3万円として、20年間運用した結果をシミュレーションする
- ランダムに10000回シミュレーションを行い、その結果を分析する
シミュレーション結果
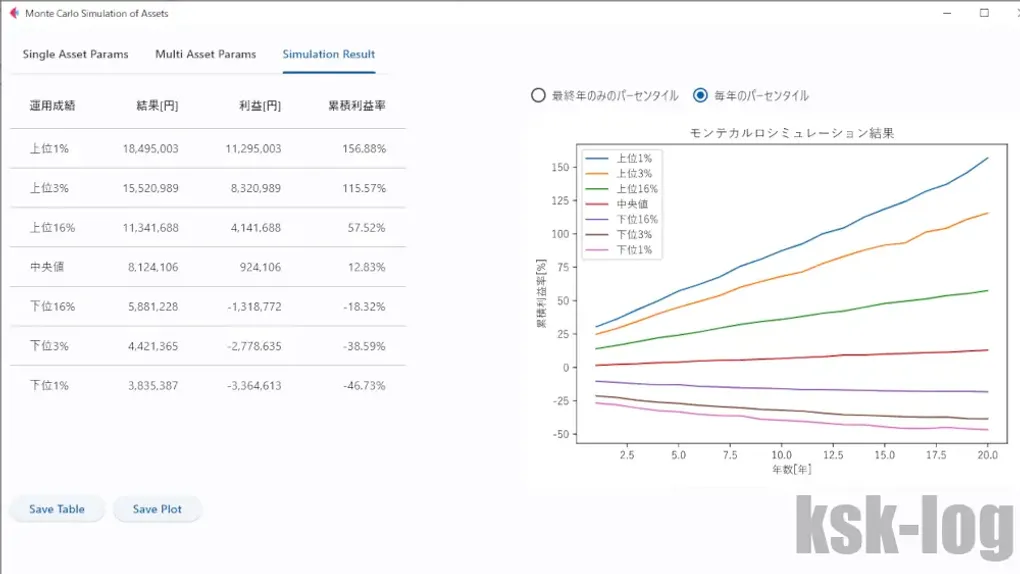
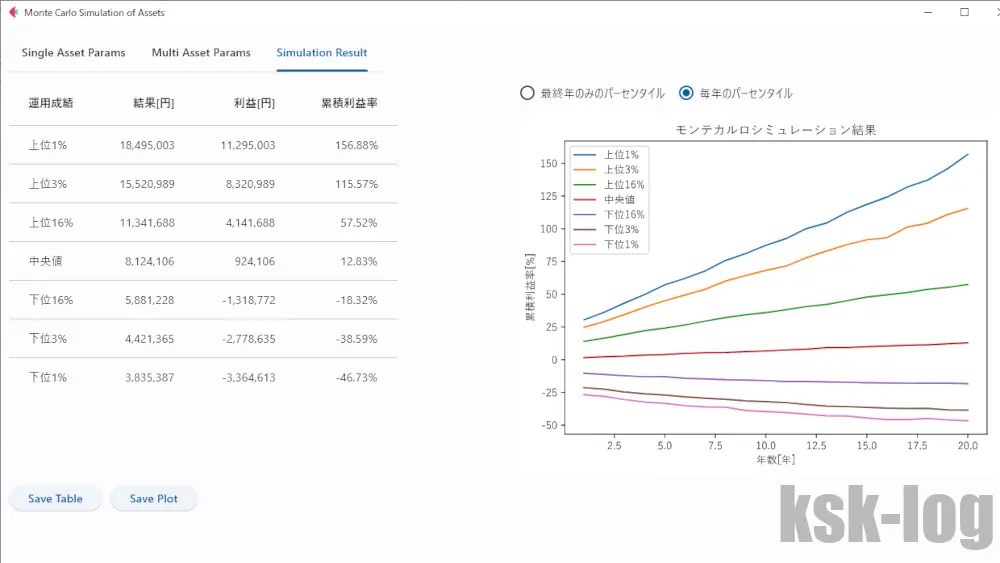
シミュレーション結果は以下のようになります。図から累積利益率を抜粋すると以下の通りです。
| 運用成績 | 累積利益率[%] |
|---|---|
| 上位1% | 156.88 |
| 上位3% | 115.57 |
| 上位16% | 57.52 |
| 中央値 | 12.83 |
| 下位16% | -18.32 |
| 下位3% | -38.59 |
| 下位1% | -46.73 |
結果の分析
これらを見てみると、中央値としては20年で12.83%の利益で、単純に20年の幾何平均をとると0.61%となります。インフレ調整後の実質リターンなので、中央値でみれば50%以上の確率で資産は実質的には目減りせず微増するということでしょうか。
逆に下位16%となると、20年で-18%と目減りすることになります。最悪のケースを引くと、下位1%では資産は46%減となるようですね。逆に上位1%の大当たりの結果を引いた場合は156%増加となるようです。
ただ、GPIFの運用は債券も半分近くある安定した運用となっているのですが、それだけ安定をとっても損をする確率が多少あるのは意外でした。これがもっとリスクの高い株式一辺倒であればもっとマイナス方面に振り切る場合もありうると考えられます。
なお、GPIFには優秀な数学系・金融系の方が多くいらっしゃるので、当然ながらこの程度のシミュレーションよりもっと高度なシミュレーションを行っているはずです。なので本シミュレーション結果でマイナスリターンの確率が多少あるといっても、彼らの高度な運用であればもっとマイナスとなる確率は低いものと思われます。
最近は情報強者なら資産運用はやっておくべき、株式一辺倒でOKみたいな話も多く聞くようになりましたが、期待値的にはプラスであってもそれなりの確率でにマイナス方向に逆ぶれする可能性もあると考えるべきでしょうかね。
ただ、今回のシミュレーションはあくまで正規分布によるランダムシミュレーションで、現実世界におけるトレンドや社会情勢などは当然ながら反映されません。なのであくまで資産運用を行った場合は期待値がプラスであってもこれだけの上下の変動がありうると覚悟はしておいて、それが許容できる範囲で資産運用を行ったほうがよかろうかと思います。
開発したツール
ソースコードおよびWindows用のexeファイルは以下のGithubリポジトリにアップロードしてあります。ツールの詳細な使い方は以下のReadmeを参照して下さい。
まとめ
- Fletとnumpyで資産運用モンテカルロシミュレーションのGUIツールを開発
- GPIFの公開資料を用いてシミュレーションを行ってみた
- 安定した資産構成であっても上振れと下振れを見ると大きな開きがある
- 資産運用を行うならこの上下振れが許容できる範囲で行うのがよさそう
スポンサーリンク